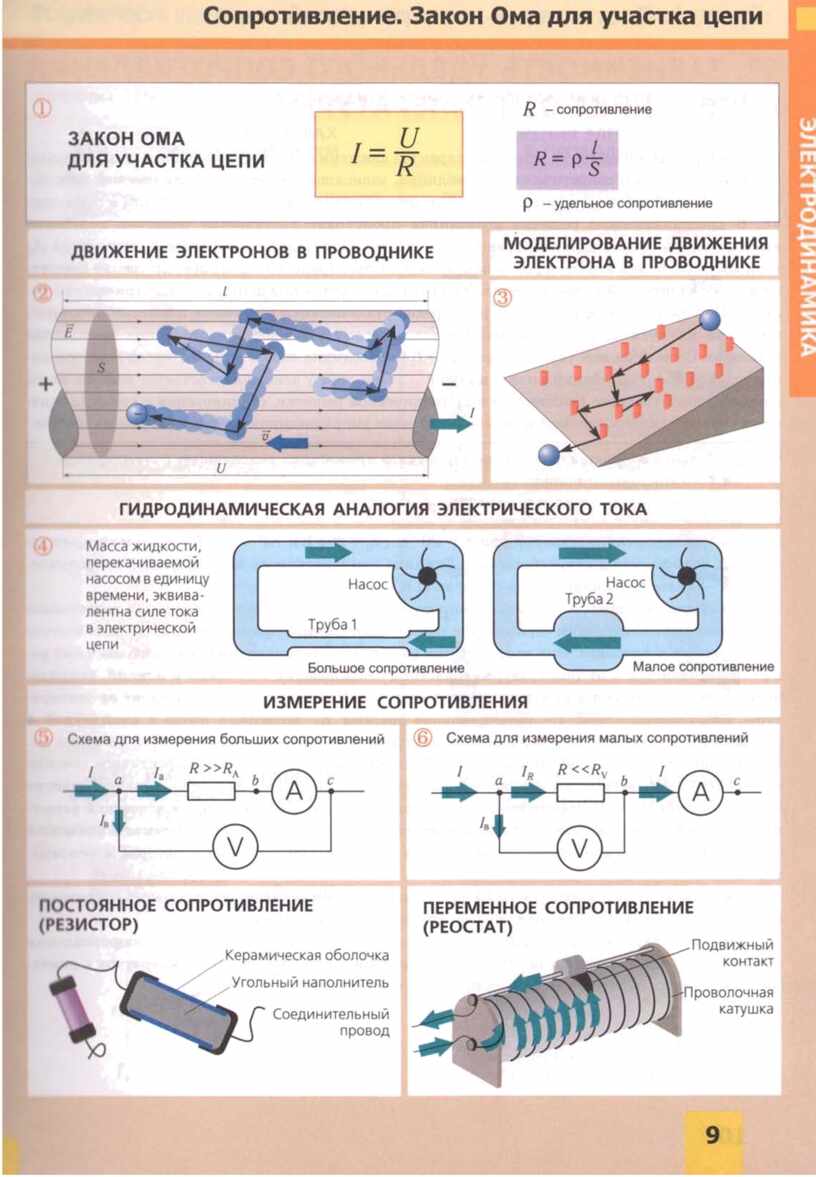
- สำหรับวงจรปิด
- แยกส่วนและวงจรไฟฟ้าที่สมบูรณ์
- การคำนวณส่วนปัจจุบันของวงจรไฟฟ้า
- ตัวเลือกการคำนวณสำหรับห่วงโซ่ที่สมบูรณ์
- ผลของกฎหมายต่อตัวแปร
- แหล่ง EMF ในวงจรที่สมบูรณ์
- R - ความต้านทานไฟฟ้า
- ส่วนที่ไม่สม่ำเสมอของวงจร DC
- การเชื่อมต่อแบบอนุกรมและแบบขนานขององค์ประกอบ
- ห่วงโซ่ขององค์ประกอบต้านทานที่เชื่อมต่อแบบอนุกรม
- ห่วงโซ่ขององค์ประกอบต้านทานที่เชื่อมต่อแบบขนาน
- รูปแบบปริพันธ์และอนุพันธ์ของกฎหมาย
- เข้าใจกระแสและแนวต้าน
- กฎของโอห์มสำหรับกระแสสลับ
- เมื่อกฎของโอห์มเกิดขึ้น
- กฎของเคิร์ชฮอฟฟ์
- แนวคิดพื้นฐาน
- ความแข็งแกร่งและความตึงเครียด
- ความต้านทานตัวนำ
- การตีความกฎหมายของโอห์ม
- การเชื่อมต่อแบบขนานและแบบอนุกรม
- การเชื่อมต่อแบบอนุกรม
- การเชื่อมต่อแบบขนาน
- อะไรทำให้เรามีการเชื่อมต่อแบบขนานและแบบอนุกรม
- แหล่ง EMF ในอุดมคติ
- ในรูปแบบดิฟเฟอเรนเชียล
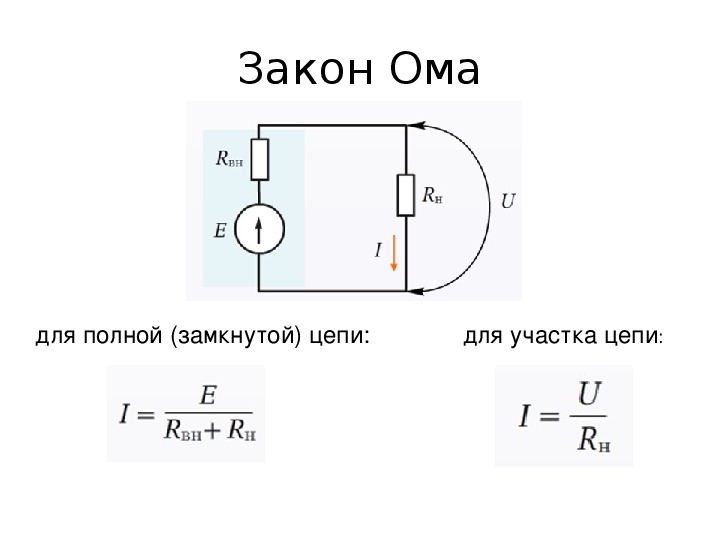
สำหรับวงจรปิด
วงจรปิดหมายถึงการเชื่อมต่อไฟฟ้าแบบปิดซึ่งกระแสหมุนเวียน เมื่อมีสายไฟต่อกันเป็นชุดและต่อวงจรจนครบจนผมวิ่งจากปลายด้านหนึ่งของวงกลมไปอีกด้านหนึ่งจะเป็นวงจรปิด
EMF (E) - แสดงและวัดเป็นโวลต์ และหมายถึงแรงดันไฟฟ้าที่เกิดจากแบตเตอรี่หรือแรงแม่เหล็กตามกฎหมายของฟาราเดย์ ซึ่งระบุว่าสนามแม่เหล็กที่แปรตามเวลาจะทำให้เกิดกระแสไฟฟ้า
จากนั้น: E = IR + Ir
E \u003d ฉัน (R + r)
ฉัน \u003d E / (R + r)
โดยที่: r คือความต้านทานของแหล่งกระแส
นิพจน์นี้เรียกว่ากฎของวงจรปิดของโอห์ม
ห่วงโซ่ที่แตกต่างกัน
แยกส่วนและวงจรไฟฟ้าที่สมบูรณ์
กฎของโอห์มที่ใช้กับส่วนใดส่วนหนึ่งหรือทั้งวงจรสามารถพิจารณาได้ในสองตัวเลือกการคำนวณ:
- แยกส่วนสั้น. เป็นส่วนหนึ่งของวงจรที่ไม่มีแหล่งกำเนิด EMF
- ห่วงโซ่ที่สมบูรณ์ประกอบด้วยหนึ่งส่วนขึ้นไป รวมถึงแหล่ง EMF ที่มีความต้านทานภายในของตัวเอง
การคำนวณส่วนปัจจุบันของวงจรไฟฟ้า
ในกรณีนี้ใช้สูตรพื้นฐาน I \u003d U / R ซึ่ง I คือความแรงของกระแส U คือแรงดันไฟฟ้า R คือความต้านทาน เราสามารถกำหนดการตีความกฎของโอห์มที่เป็นที่ยอมรับโดยทั่วไปได้:
สูตรนี้เป็นพื้นฐานสำหรับสูตรอื่นๆ มากมายที่นำเสนอเกี่ยวกับสิ่งที่เรียกว่า "คาโมมายล์" ในการออกแบบกราฟิก ในภาค P - กำลังถูกกำหนดในภาค I, U และ R - การดำเนินการที่เกี่ยวข้องกับความแรงกระแสแรงดันและความต้านทานในปัจจุบัน
แต่ละนิพจน์ - ทั้งแบบพื้นฐานและแบบเพิ่มเติมช่วยให้คุณสามารถคำนวณพารามิเตอร์ที่แน่นอนขององค์ประกอบที่มีไว้สำหรับใช้ในวงจร
ผู้เชี่ยวชาญที่ทำงานเกี่ยวกับวงจรไฟฟ้าจะทำการกำหนดพารามิเตอร์อย่างรวดเร็วโดยใช้วิธีสามเหลี่ยมที่แสดงในรูป
การคำนวณควรคำนึงถึงความต้านทานของตัวนำที่เชื่อมต่อกับองค์ประกอบของส่วน เนื่องจากทำจากวัสดุที่แตกต่างกัน พารามิเตอร์นี้จะแตกต่างกันในแต่ละกรณีหากจำเป็นต้องสร้างวงจรที่สมบูรณ์ สูตรหลักจะเสริมด้วยพารามิเตอร์ของแหล่งจ่ายแรงดันไฟ เช่น แบตเตอรี่
ตัวเลือกการคำนวณสำหรับห่วงโซ่ที่สมบูรณ์
วงจรที่สมบูรณ์ประกอบด้วยแต่ละส่วน รวมกันเป็นวงจรเดียวพร้อมกับแหล่งจ่ายแรงดันไฟ (EMF) ดังนั้นความต้านทานที่มีอยู่ของส่วนต่างๆ จึงเสริมด้วยความต้านทานภายในของแหล่งที่เชื่อมต่อ ดังนั้นการตีความหลักที่กล่าวถึงก่อนหน้านี้จะอ่านดังนี้: I = U / (R + r) มีการเพิ่มเลขชี้กำลังความต้านทาน (r) ของแหล่ง EMF ที่นี่แล้ว
จากมุมมองของฟิสิกส์บริสุทธิ์ ตัวบ่งชี้นี้ถือเป็นค่าที่น้อยมาก อย่างไรก็ตามในทางปฏิบัติเมื่อทำการคำนวณวงจรและวงจรที่ซับซ้อน ผู้เชี่ยวชาญจำเป็นต้องคำนึงถึงเนื่องจากการต้านทานเพิ่มเติมส่งผลต่อความถูกต้องของงาน นอกจากนี้ โครงสร้างของแต่ละแหล่งต่างกันมาก ส่งผลให้ความต้านทานในบางกรณีสามารถแสดงได้ด้วยอัตราที่ค่อนข้างสูง
การคำนวณข้างต้นดำเนินการตามวงจรไฟฟ้ากระแสตรง การดำเนินการและการคำนวณด้วยกระแสสลับจะทำขึ้นตามรูปแบบที่แตกต่างกัน
ผลของกฎหมายต่อตัวแปร
ด้วยกระแสสลับ ความต้านทานของวงจรจะเรียกว่าอิมพีแดนซ์ ซึ่งประกอบด้วยความต้านทานเชิงแอคทีฟและโหลดตัวต้านทานแบบรีแอกทีฟ เนื่องจากการมีอยู่ขององค์ประกอบที่มีคุณสมบัติอุปนัยและค่ากระแสไซน์ แรงดันก็เป็นตัวแปรเช่นกัน ซึ่งทำหน้าที่ตามกฎหมายสวิตชิ่ง
ดังนั้นการออกแบบวงจรไฟฟ้ากระแสสลับของกฎของโอห์มจึงคำนวณโดยคำนึงถึงผลกระทบเฉพาะ: นำหรือล้าหลังขนาดของกระแสจากแรงดันไฟฟ้าตลอดจนการปรากฏตัวของพลังงานที่ใช้งานและปฏิกิริยาในทางกลับกัน ค่ารีแอกแตนซ์รวมถึงส่วนประกอบอุปนัยหรือตัวเก็บประจุ
ปรากฏการณ์ทั้งหมดเหล่านี้จะสอดคล้องกับสูตร Z \u003d U / I หรือ Z \u003d R + J * (XL - XC) โดยที่ Z คืออิมพีแดนซ์ R - โหลดที่ใช้งาน; XL, XC - โหลดอุปนัยและ capacitive; J เป็นปัจจัยแก้ไข
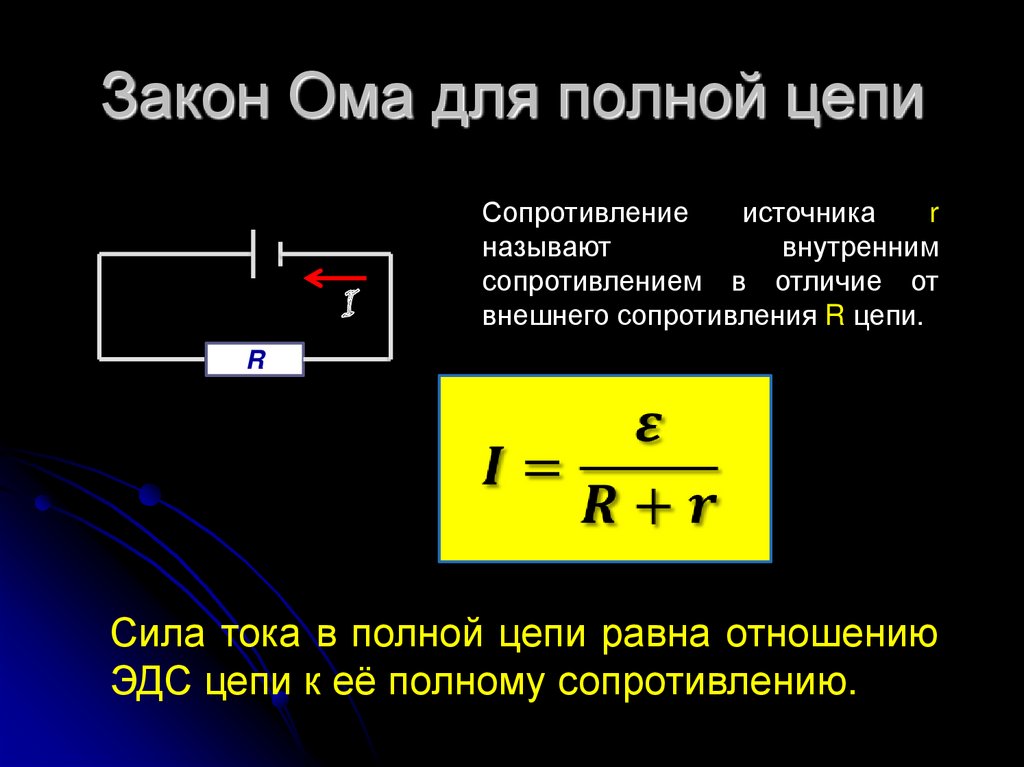
แหล่ง EMF ในวงจรที่สมบูรณ์
สำหรับการเกิดขึ้นของกระแสไฟฟ้าในวงจรปิด วงจรนี้จะต้องมีองค์ประกอบพิเศษอย่างน้อยหนึ่งองค์ประกอบซึ่งจะมีการถ่ายโอนประจุระหว่างขั้วของมัน แรงที่บรรทุกประจุภายในองค์ประกอบนี้กระทำต่อสนามไฟฟ้า ซึ่งหมายความว่าธรรมชาติของพวกมันจะต้องแตกต่างจากไฟฟ้า ดังนั้นกองกำลังดังกล่าวจึงเรียกว่าบุคคลที่สาม
ข้าว. 1. แรงภายนอกในวิชาฟิสิกส์
องค์ประกอบของวงจรไฟฟ้าที่แรงภายนอกทำงานเพื่อถ่ายเทประจุกับการกระทำของสนามไฟฟ้าเรียกว่าแหล่งกำเนิดกระแส ลักษณะสำคัญของมันคือขนาดของแรงภายนอก ในการอธิบายลักษณะนี้ จึงมีการแนะนำมาตรการพิเศษ - แรงเคลื่อนไฟฟ้า (EMF) ซึ่งเขียนแทนด้วยตัวอักษร $\mathscr{E}$
ค่า EMF ของแหล่งจ่ายปัจจุบันเท่ากับอัตราส่วนของแรงภายนอกสำหรับการถ่ายโอนประจุไปยังมูลค่าของประจุนี้:
$$\mathscr{E}={A_{st}\over q}$$
เนื่องจากความหมายของ EMF นั้นใกล้เคียงกับความหมายของแรงดันไฟฟ้ามาก (จำได้ว่า แรงดันคืออัตราส่วนของงานที่ทำโดยสนามไฟฟ้าที่นำประจุมาสู่ค่าของประจุนี้) ดังนั้น EMF ก็เหมือนกับแรงดันที่วัดใน โวลต์:
$$1B={J\overCl}$$
ลักษณะทางไฟฟ้าที่สำคัญที่สุดอันดับสองของแหล่งกำเนิดกระแสไฟฟ้าจริงคือความต้านทานภายในเมื่อประจุถูกถ่ายโอนระหว่างขั้ว ประจุจะมีปฏิกิริยากับสารของแหล่งกำเนิด EMF ดังนั้น แหล่งกำเนิดของกระแสไฟฟ้าจึงมีความต้านทานอยู่บ้าง ความต้านทานภายใน เช่นเดียวกับความต้านทานทั่วไป วัดเป็นโอห์ม แต่เขียนแทนด้วยตัวอักษรละตินตัวเล็ก $r$

ข้าว. 2. ตัวอย่างแหล่งที่มาปัจจุบัน
R - ความต้านทานไฟฟ้า
ความต้านทานเป็นส่วนกลับของแรงดันไฟฟ้าและสามารถเปรียบเทียบได้กับผลของการเคลื่อนไหวร่างกายกับการเคลื่อนไหวในน้ำไหล หน่วยของ R คือ Om ซึ่งเขียนแทนด้วยอักษรกรีกตัวพิมพ์ใหญ่ Omega
ส่วนกลับของความต้านทาน (1/R) เรียกว่าการนำไฟฟ้า ซึ่งวัดความสามารถของวัตถุในการนำประจุ แสดงเป็นหน่วยของซีเมนส์
ปริมาณอิสระทางเรขาคณิตที่ใช้เรียกว่า สภาพต้านทาน และมักแสดงด้วยสัญลักษณ์กรีก r
ข้อมูลเพิ่มเติม. กฎของโอห์มช่วยสร้างตัวบ่งชี้ที่สำคัญสามประการของการทำงานของเครือข่ายไฟฟ้า ซึ่งทำให้การคำนวณพลังงานง่ายขึ้น ใช้ไม่ได้กับเครือข่ายด้านเดียวที่มีองค์ประกอบ เช่น ไดโอด ทรานซิสเตอร์ และอื่นๆ และยังใช้ไม่ได้กับองค์ประกอบที่ไม่เป็นเชิงเส้นซึ่งมีไทริสเตอร์เป็นตัวอย่าง เนื่องจากค่าความต้านทานขององค์ประกอบเหล่านี้เปลี่ยนแปลงไปตามแรงดันและกระแสที่กำหนด
ที่ความถี่สูง พฤติกรรมแบบกระจายจะกลายเป็นส่วนสำคัญ สิ่งเดียวกันนี้เกิดขึ้นกับสายไฟที่ยาวมาก แม้ที่ความถี่ต่ำถึง 60 Hz สายส่งที่ยาวมาก เช่น 30 กม. ก็มีลักษณะแบบกระจายสาเหตุหลักคือสัญญาณไฟฟ้าที่มีประสิทธิภาพซึ่งแพร่กระจายในวงจรคือคลื่นแม่เหล็กไฟฟ้า ไม่ใช่โวลต์และแอมแปร์ซึ่งติดโดยคลื่นแม่เหล็กไฟฟ้า ตัวนำเพียงแค่ทำหน้าที่เป็นแนวทางสำหรับคลื่น ตัวอย่างเช่น สายโคแอกเชียลจะแสดงค่า Z = 75 โอห์ม แม้ว่าค่าความต้านทานกระแสตรงจะน้อยมากก็ตาม
กฎของโอห์มเป็นกฎพื้นฐานของวิศวกรรมไฟฟ้า มีการใช้งานจริงจำนวนมากในวงจรไฟฟ้าและส่วนประกอบอิเล็กทรอนิกส์ทั้งหมด
ตัวอย่างทั่วไปของการประยุกต์ใช้กฎของโอห์ม:
- กำลังจ่ายให้กับเครื่องทำความร้อนไฟฟ้า เมื่อพิจารณาถึงความต้านทานของคอยล์ฮีตเตอร์และแรงดันไฟฟ้าที่ใช้ พลังงานที่จ่ายให้กับฮีตเตอร์นั้นสามารถคำนวณได้
- ทางเลือกของฟิวส์ เป็นส่วนประกอบป้องกันที่เชื่อมต่อแบบอนุกรมกับอุปกรณ์อิเล็กทรอนิกส์ ฟิวส์/CB ได้รับการจัดอันดับเป็นแอมป์ อัตราฟิวส์ปัจจุบันคำนวณโดยใช้กฎของโอห์ม
- การออกแบบอุปกรณ์อิเล็คทรอนิคส์ อุปกรณ์อิเล็กทรอนิกส์ เช่น แล็ปท็อปและโทรศัพท์มือถือ ต้องใช้แหล่งจ่ายไฟ DC ที่มีพิกัดกระแสไฟเฉพาะ แบตเตอรี่โทรศัพท์มือถือทั่วไปต้องใช้ 0.7-1A ตัวต้านทานจะใช้เพื่อควบคุมอัตราการไหลของกระแสผ่านส่วนประกอบเหล่านี้ กฎของโอห์มใช้ในการคำนวณกระแสไฟในวงจรทั่วไป
มีอยู่ครั้งหนึ่ง ข้อสรุปของโอห์มกลายเป็นตัวเร่งปฏิกิริยาสำหรับการวิจัยใหม่ในสาขาไฟฟ้า และวันนี้พวกเขาไม่ได้สูญเสียความสำคัญของมันไป เนื่องจากวิศวกรรมไฟฟ้าสมัยใหม่ใช้หลักการเหล่านี้ ในปี 1841 Om ได้รับรางวัลเกียรติยศสูงสุดของ Royal Society นั่นคือเหรียญ Copley และคำว่า "Om" ได้รับการยอมรับว่าเป็นหน่วยต่อต้านตั้งแต่ช่วงปี 1872
ส่วนที่ไม่สม่ำเสมอของวงจร DC
โครงสร้างที่ต่างกันมีส่วนของวงจรซึ่งนอกจากตัวนำและองค์ประกอบแล้วยังมีแหล่งกระแส ต้องคำนึงถึง EMF ของมันด้วยเมื่อคำนวณความแรงของกระแสรวมในบริเวณนี้
มีสูตรที่กำหนดพารามิเตอร์หลักและกระบวนการของไซต์ที่ต่างกัน: q = q0 x n x V. ตัวบ่งชี้มีลักษณะดังนี้:
- ในกระบวนการเคลื่อนย้ายประจุ (q) พวกมันจะได้รับความหนาแน่นที่แน่นอน ประสิทธิภาพของมันขึ้นอยู่กับความแรงของกระแสและพื้นที่หน้าตัดของตัวนำ (S)
- ภายใต้เงื่อนไขของความเข้มข้นที่แน่นอน (n) เป็นไปได้ที่จะระบุจำนวนหน่วยประจุ (q0) ที่ถูกย้ายในช่วงเวลาเดียวอย่างแม่นยำ
- สำหรับการคำนวณ ตัวนำไฟฟ้าถือเป็นส่วนทรงกระบอกที่มีปริมาตร (V) ตามเงื่อนไข
เมื่อต่อตัวนำเข้ากับแบตเตอรี่ แบตเตอรีจะถูกคายประจุหลังจากนั้นครู่หนึ่ง นั่นคือการเคลื่อนที่ของอิเล็กตรอนจะค่อย ๆ ช้าลงและในที่สุดก็หยุดพร้อมกัน สิ่งนี้อำนวยความสะดวกโดยโครงตาข่ายโมเลกุลของตัวนำซึ่งต่อต้านการชนกันของอิเล็กตรอนระหว่างกันและปัจจัยอื่นๆ เพื่อเอาชนะการต่อต้านดังกล่าว กองกำลังของบุคคลที่สามจะต้องใช้เพิ่มเติม
ระหว่างการคำนวณ แรงเหล่านี้จะถูกเพิ่มเข้าไปในหน่วยคูลอมบ์ นอกจากนี้ในการถ่ายโอนหน่วยประจุ q จากจุดที่ 1 ไปยังจุดที่ 2 จำเป็นต้องดำเนินการ A1-2 หรือเพียงแค่ A12 เพื่อจุดประสงค์นี้ ความต่างศักย์ (ϕ1 - ϕ2) จะถูกสร้างขึ้น ภายใต้การกระทำของแหล่งกระแสตรง EMF เกิดขึ้นโดยเคลื่อนที่ประจุไปตามวงจร ขนาดของความเค้นทั้งหมดจะประกอบด้วยแรงทั้งหมดที่ระบุไว้ข้างต้น
ต้องคำนึงถึงขั้วของการเชื่อมต่อกับแหล่งจ่ายไฟ DC ในการคำนวณ เมื่อเปลี่ยนขั้ว EMF ก็จะเปลี่ยน เร่งหรือชะลอการเคลื่อนที่ของประจุ
การเชื่อมต่อแบบอนุกรมและแบบขนานขององค์ประกอบ
สำหรับองค์ประกอบของวงจรไฟฟ้า (ส่วนของวงจร) โมเมนต์เฉพาะคือการเชื่อมต่อแบบอนุกรมหรือแบบขนาน
ดังนั้นการเชื่อมต่อแต่ละประเภทจึงมีลักษณะที่แตกต่างกันของกระแสและการจ่ายแรงดันไฟ ในบัญชีนี้ กฎของโอห์มยังนำไปใช้ในรูปแบบต่างๆ ขึ้นอยู่กับตัวเลือกในการรวมองค์ประกอบด้วย
ห่วงโซ่ขององค์ประกอบต้านทานที่เชื่อมต่อแบบอนุกรม
สำหรับการเชื่อมต่อแบบอนุกรม (ส่วนของวงจรที่มีสององค์ประกอบ) จะใช้ถ้อยคำ:
- ฉัน = ฉัน1 = ฉัน2 ;
- ยู = ยู1 + คุณ2 ;
- R=R1 + ร2
สูตรนี้แสดงให้เห็นชัดเจนว่า กระแสที่ไหลในส่วนของวงจรจะไม่เปลี่ยนค่าโดยไม่คำนึงถึงจำนวนของส่วนประกอบต้านทานที่เชื่อมต่อแบบอนุกรม
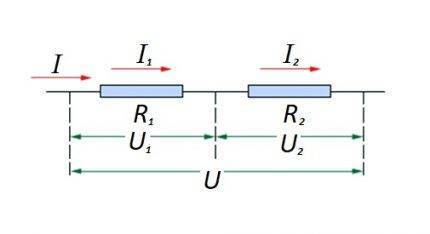 การเชื่อมต่อองค์ประกอบต้านทานในส่วนวงจรต่ออนุกรมกัน ตัวเลือกนี้มีกฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบต้านทาน; U, U1, U2 - แรงดันไฟฟ้าที่ใช้
การเชื่อมต่อองค์ประกอบต้านทานในส่วนวงจรต่ออนุกรมกัน ตัวเลือกนี้มีกฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบต้านทาน; U, U1, U2 - แรงดันไฟฟ้าที่ใช้
ปริมาณแรงดันไฟฟ้าที่ใช้กับส่วนประกอบตัวต้านทานแบบแอคทีฟของวงจรคือผลรวมและบวกเข้ากับค่าของแหล่งกำเนิด EMF
ในกรณีนี้ แรงดันไฟฟ้าของแต่ละส่วนประกอบคือ: Ux = I * Rx
ความต้านทานรวมควรพิจารณาเป็นผลรวมของค่าของส่วนประกอบความต้านทานทั้งหมดของวงจร
ห่วงโซ่ขององค์ประกอบต้านทานที่เชื่อมต่อแบบขนาน
ในกรณีที่มีการเชื่อมต่อแบบขนานของส่วนประกอบต้านทาน สูตรนี้ถือว่ายุติธรรมโดยคำนึงถึงกฎหมายของโอห์มนักฟิสิกส์ชาวเยอรมัน:
- ฉัน = ฉัน1 + ฉัน2 … ;
- ยู = ยู1 = คุณ2 … ;
- 1/R = 1/R1 +1 / R2 + …
ตัวเลือกสำหรับการรวบรวมส่วนวงจรของประเภท "ผสม" จะไม่ถูกแยกออกเมื่อใช้การเชื่อมต่อแบบขนานและแบบอนุกรม
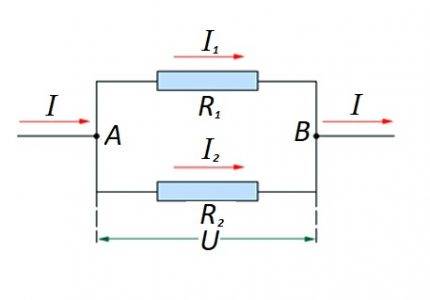 การเชื่อมต่อขององค์ประกอบต้านทานในส่วนวงจรขนานกัน สำหรับตัวเลือกนี้ จะใช้กฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบต้านทาน; U - แรงดันไฟฟ้าที่ใช้; A, B - จุดเข้า / ออก
การเชื่อมต่อขององค์ประกอบต้านทานในส่วนวงจรขนานกัน สำหรับตัวเลือกนี้ จะใช้กฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบต้านทาน; U - แรงดันไฟฟ้าที่ใช้; A, B - จุดเข้า / ออก
สำหรับตัวเลือกดังกล่าว การคำนวณมักจะดำเนินการโดยการคำนวณเริ่มต้นของพิกัดความต้านทานของการเชื่อมต่อแบบขนาน จากนั้นค่าของตัวต้านทานที่เชื่อมต่อแบบอนุกรมจะถูกเพิ่มเข้ากับผลลัพธ์
รูปแบบปริพันธ์และอนุพันธ์ของกฎหมาย
จุดทั้งหมดข้างต้นพร้อมการคำนวณใช้ได้กับเงื่อนไขเมื่อใช้ตัวนำของโครงสร้าง "ที่เป็นเนื้อเดียวกัน" เป็นส่วนหนึ่งของวงจรไฟฟ้า
ในขณะเดียวกัน ในทางปฏิบัติ เรามักจะต้องจัดการกับการสร้างแผนผัง ซึ่งโครงสร้างของตัวนำเปลี่ยนแปลงไปในด้านต่างๆ ตัวอย่างเช่นใช้ลวดที่มีหน้าตัดที่ใหญ่กว่าหรือในทางกลับกันลวดที่เล็กกว่านั้นทำจากวัสดุที่แตกต่างกัน
เพื่อพิจารณาความแตกต่างดังกล่าว จึงมีรูปแบบที่เรียกว่า สำหรับตัวนำขนาดเล็กที่ไม่สิ้นสุด ระดับความหนาแน่นกระแสจะคำนวณโดยขึ้นอยู่กับความเข้มและค่าการนำไฟฟ้า
ภายใต้การคำนวณส่วนต่างจะใช้สูตร: J = ό * E
สำหรับการคำนวณอินทิกรัลตามลำดับ สูตร: I * R = φ1 - φ2 + έ
อย่างไรก็ตาม ตัวอย่างเหล่านี้ค่อนข้างใกล้กับโรงเรียนคณิตศาสตร์ระดับอุดมศึกษาและไม่ได้ใช้จริงในการปฏิบัติงานจริงของช่างไฟฟ้าทั่วไป
เข้าใจกระแสและแนวต้าน
เริ่มจากแนวคิดเรื่องกระแสไฟฟ้ากันก่อนกล่าวโดยสรุป กระแสไฟฟ้าที่สัมพันธ์กับโลหะคือการเคลื่อนที่โดยตรงของอิเล็กตรอน ซึ่งเป็นอนุภาคที่มีประจุลบ มักจะแสดงเป็นวงกลมขนาดเล็ก ในสภาวะที่สงบ พวกมันจะเคลื่อนที่แบบสุ่มและเปลี่ยนทิศทางตลอดเวลา ภายใต้เงื่อนไขบางประการ - การปรากฏตัวของความแตกต่างที่อาจเกิดขึ้น - อนุภาคเหล่านี้เริ่มเคลื่อนที่ในทิศทางใดทิศทางหนึ่ง การเคลื่อนที่นี้เป็นกระแสไฟฟ้า
เพื่อให้ชัดเจนขึ้น เราสามารถเปรียบเทียบอิเล็กตรอนกับน้ำที่หกบนระนาบบางลำ ตราบใดที่เครื่องบินอยู่นิ่ง น้ำก็ไม่เคลื่อนที่ แต่ทันทีที่มีความลาดชันปรากฏขึ้น (ความต่างที่อาจเกิดขึ้น) น้ำก็เริ่มเคลื่อนตัว เหมือนกันกับอิเล็กตรอน
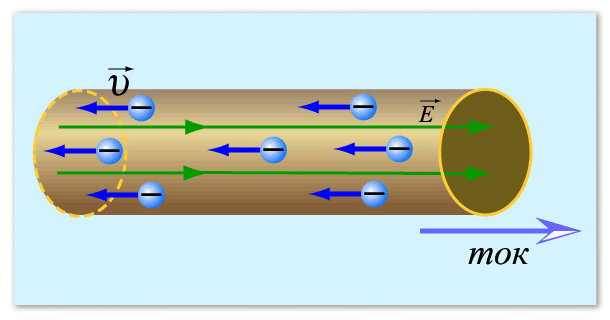
นี่คือวิธีที่สามารถจินตนาการถึงกระแสไฟฟ้าได้
ตอนนี้เราต้องเข้าใจว่าการต่อต้านคืออะไรและทำไมพวกมันถึงมีกระแสย้อนกลับด้วยความแข็งแกร่งในปัจจุบัน: ยิ่งความต้านทานสูง กระแสก็จะยิ่งต่ำลง ดังที่คุณทราบ อิเล็กตรอนเคลื่อนที่ผ่านตัวนำ โดยปกติแล้วจะเป็นลวดโลหะ เนื่องจากโลหะสามารถนำไฟฟ้าได้ดี เรารู้ว่าโลหะมีตาข่ายคริสตัลหนาแน่น: อนุภาคจำนวนมากที่อยู่ใกล้และเชื่อมต่อถึงกัน อิเล็กตรอนที่เคลื่อนที่ไปมาระหว่างอะตอมของโลหะชนกับพวกมัน ซึ่งทำให้พวกมันเคลื่อนที่ได้ยาก สิ่งนี้ช่วยแสดงให้เห็นความต้านทานที่ตัวนำกระทำ ตอนนี้มันชัดเจนว่าเหตุใดยิ่งความต้านทานสูง ความแรงของกระแสไฟฟ้ายิ่งต่ำ ยิ่งมีอนุภาคมาก ยิ่งยากสำหรับอิเล็กตรอนที่จะเอาชนะเส้นทาง พวกมันจะทำได้ช้ากว่า นี้ดูเหมือนว่าจะได้รับการแยกออก
หากคุณต้องการทดสอบการพึ่งพาอาศัยกันนี้โดยสังเกตจากประสบการณ์ ให้ค้นหาตัวต้านทานแบบปรับค่าได้ ต่อตัวต้านทานแบบอนุกรม - แอมมิเตอร์ - แหล่งกระแส (แบตเตอรี่)ขอแนะนำให้ใส่สวิตช์เข้าไปในวงจร - สวิตช์สลับธรรมดา
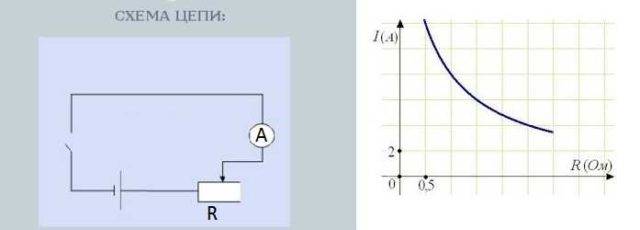
วงจรทดสอบการพึ่งพากระแสบนความต้านทาน
การหมุนลูกบิดตัวต้านทานจะเปลี่ยนความต้านทาน ในขณะเดียวกัน การอ่านค่าแอมมิเตอร์ซึ่งวัดความแรงของกระแสก็เปลี่ยนไปเช่นกัน ยิ่งไปกว่านั้น ยิ่งมีความต้านทานมากเท่าใด ลูกธนูก็จะยิ่งเบี่ยงเบนน้อยลงเท่านั้น - กระแสไฟก็จะยิ่งน้อยลง ยิ่งความต้านทานต่ำ ลูกศรยิ่งเบี่ยงเบน - กระแสยิ่งมากขึ้น
การพึ่งพากระแสบนแนวต้านนั้นเกือบจะเป็นเส้นตรง กล่าวคือ มันสะท้อนบนกราฟเป็นเส้นตรงเกือบ ทำไมเกือบ - ควรพูดคุยแยกกัน แต่นั่นเป็นอีกเรื่องหนึ่ง
กฎของโอห์มสำหรับกระแสสลับ
เมื่อคำนวณวงจรไฟฟ้ากระแสสลับ แทนที่จะใช้แนวคิดของความต้านทาน แนวคิดของ "อิมพีแดนซ์" ถูกนำมาใช้ อิมพีแดนซ์แสดงด้วยตัวอักษร Z ซึ่งรวมถึงความต้านทานเชิงแอ็คทีฟของโหลด Rเอ และรีแอกแตนซ์ X (หรือ Rr). นี่เป็นเพราะรูปร่างของกระแสไซน์ (และกระแสของรูปแบบอื่น ๆ ) และพารามิเตอร์ขององค์ประกอบอุปนัยเช่นเดียวกับกฎการสลับ:
- กระแสในวงจรอุปนัยไม่สามารถเปลี่ยนแปลงได้ในทันที
- แรงดันไฟฟ้าในวงจรที่มีความจุไม่สามารถเปลี่ยนแปลงได้ในทันที
ดังนั้นกระแสจึงเริ่มล้าหลังหรือนำไปสู่แรงดันไฟฟ้า และกำลังไฟฟ้าที่ปรากฏจะถูกแบ่งออกเป็นแบบแอคทีฟและแบบรีแอกทีฟ
U=I/Z
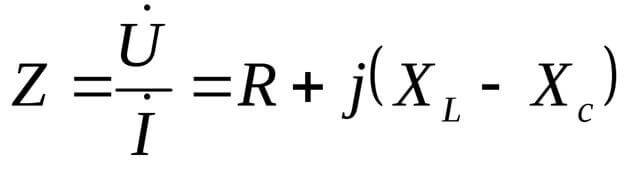
Xหลี่ และ Xค เป็นส่วนประกอบปฏิกิริยาของโหลด
ในเรื่องนี้แนะนำค่าcosФ:
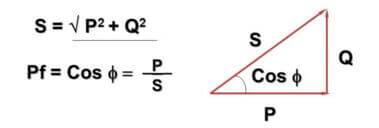
ที่นี่ - Q - กำลังไฟฟ้ารีแอกทีฟเนื่องจากส่วนประกอบกระแสสลับและอุปนัย - คาปาซิทีฟ, P - พลังงานที่ใช้งาน (กระจายในส่วนประกอบที่ใช้งาน), S - กำลังปรากฏ, cosF - ตัวประกอบกำลัง
คุณอาจสังเกตเห็นว่าสูตรและการแทนค่าของสูตรตัดกับทฤษฎีบทพีทาโกรัส นี่เป็นความจริงและมุม Ф ขึ้นอยู่กับขนาดของส่วนประกอบปฏิกิริยาของโหลด - ยิ่งมีขนาดใหญ่เท่าใดก็ยิ่งมีขนาดใหญ่เท่านั้นในทางปฏิบัติสิ่งนี้นำไปสู่ความจริงที่ว่ากระแสที่ไหลจริงในเครือข่ายนั้นมากกว่าที่คำนึงถึงโดยมาตรวัดในครัวเรือนในขณะที่องค์กรจ่ายเต็มกำลัง
ในกรณีนี้ ค่าความต้านทานจะแสดงในรูปแบบที่ซับซ้อน:
ในที่นี้ j คือหน่วยจินตภาพ ซึ่งเป็นเรื่องปกติสำหรับรูปแบบสมการที่ซับซ้อน โดยทั่วไปเรียกน้อยกว่าว่า i แต่ในทางวิศวกรรมไฟฟ้า ค่าประสิทธิผลของกระแสสลับยังแสดงอยู่ด้วย ดังนั้น เพื่อไม่ให้สับสน ควรใช้ j
หน่วยจินตภาพคือ √-1 มีเหตุผลที่ไม่มีตัวเลขดังกล่าวเมื่อยกกำลังสอง ซึ่งอาจส่งผลให้ผลลัพธ์เป็นลบเป็น "-1"
เมื่อกฎของโอห์มเกิดขึ้น
การสร้างเงื่อนไขในอุดมคติไม่ใช่เรื่องง่าย แม้ในตัวนำบริสุทธิ์ ความต้านทานไฟฟ้าจะแปรผันตามอุณหภูมิ การลดลงช่วยลดกิจกรรมของโมเลกุลของตะแกรงคริสตัลซึ่งทำให้การเคลื่อนที่ของประจุฟรีง่ายขึ้น ที่ระดับ "เยือกแข็ง" ระดับหนึ่งจะเกิดผลกระทบของตัวนำยิ่งยวด เมื่อถูกความร้อนจะเกิดผลตรงกันข้าม (การเสื่อมสภาพของการนำไฟฟ้า)
ในเวลาเดียวกัน อิเล็กโทรไลต์ โลหะ และเซรามิกบางชนิดยังคงมีความต้านทานไฟฟ้าโดยไม่คำนึงถึงความหนาแน่นของกระแสไฟ ความเสถียรของพารามิเตอร์ในขณะที่ยังคงรักษาอุณหภูมิไว้ทำให้สามารถใช้สูตรของกฎของโอห์มได้โดยไม่ต้องแก้ไขเพิ่มเติม
วัสดุเซมิคอนดักเตอร์และก๊าซมีลักษณะความต้านทานไฟฟ้าที่แตกต่างกัน พารามิเตอร์นี้ได้รับผลกระทบอย่างมากจากความเข้มของกระแสในระดับเสียงควบคุม ในการคำนวณลักษณะการทำงาน ต้องใช้วิธีการคำนวณแบบพิเศษ
หากพิจารณาจากกระแสสลับ วิธีการคำนวณจะได้รับการแก้ไขในกรณีนี้จะต้องคำนึงถึงการมีอยู่ของส่วนประกอบที่ทำปฏิกิริยา ด้วยลักษณะความต้านทานของความต้านทาน จึงเป็นไปได้ที่จะใช้เทคโนโลยีการคำนวณที่พิจารณาตามสูตรของกฎของโอห์ม
กฎของเคิร์ชฮอฟฟ์
การกระจาย
กระแสในกิ่งของวงจรไฟฟ้า
ปฏิบัติตามกฎข้อที่หนึ่งของ Kirchhoff
และการกระจายความเครียดในส่วนต่างๆ
เชนปฏิบัติตามกฎข้อที่สองของ Kirchhoff
กฎของเคิร์ชฮอฟฟ์
ร่วมกับกฎของโอห์มเป็นหลัก
ในทฤษฎีวงจรไฟฟ้า
ครั้งแรก
กฎของเคอร์ชอฟฟ์:
พีชคณิต
ผลรวมของกระแสในโหนดเป็นศูนย์:
ผม
= 0 (19)
ที่ไหน
ผม
คือจำนวนสาขาที่มาบรรจบกันที่โหนดที่กำหนด
นั่นคือ ผลรวม
แผ่ขยายไปตามกระแสน้ำในกิ่งก้าน
ซึ่งมาบรรจบกันในการพิจารณา
โหนด
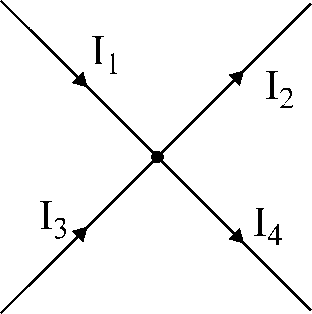
รูปที่ 17 ภาพประกอบ
กฎข้อที่หนึ่งของ Kirchhoff
ตัวเลข
สมการที่รวบรวมตามครั้งแรก
กฎของ Kirchhoff ถูกกำหนดโดยสูตร:
นู๋
= นู๋
– 1,
ที่ไหน
หนู
คือจำนวนโหนดในสายที่พิจารณา
สัญญาณของกระแสน้ำใน
โดยคำนึงถึงสมการที่เลือกไว้
ทิศทางบวก ป้ายที่
กระแสจะเท่ากันหากกระแสเท่ากัน
เชิงสัมพันธ์กับสิ่งนี้
โหนด
ตัวอย่างเช่น,
สำหรับโหนดที่แสดงในรูปที่ 17:
เรากำหนดสัญญาณให้กับกระแสที่ไหลไปยังโหนด
"+" และกระแสน้ำที่ไหลจากโหนด - สัญญาณ
«-».
แล้วสมการ
ตามกฎข้อที่หนึ่งของ Kirchhoff จะเขียนว่า
ดังนั้น:
ฉัน1
- ฉัน2
+ ฉัน3
- ฉัน4
= 0.
สมการ
รวบรวมตามกฎข้อที่หนึ่งของ Kirchhoff
เรียกว่าโหนด
นี้
กฎหมายเป็นการแสดงออกถึงความจริงที่ว่าในโหนด
ประจุไฟฟ้าไม่สะสม
และไม่ถูกบริโภค ปริมาณไฟฟ้า
ค่าใช้จ่ายที่มายังไซต์เท่ากับยอดรวม
ค่าใช้จ่ายออกจากโหนดในที่เดียว
ช่วงเวลาเดียวกัน
ที่สอง
กฎของเคอร์ชอฟฟ์:
พีชคณิต
ผลรวมของแรงเคลื่อนไฟฟ้า ในวงจรปิดใด ๆ
ห่วงโซ่มีค่าเท่ากับผลรวมเชิงพีชคณิตของน้ำตก
แรงดันไฟฟ้าบนองค์ประกอบของวงจรนี้:
อุย
=
ไอ
IiRi=Ei(20)
ที่ไหน
ผม
- หมายเลของค์ประกอบ (ความต้านทานหรือ
แหล่งกำเนิดแรงดันไฟฟ้า) ในการพิจารณา
รูปร่าง
**ตัวเลข
สมการที่รวบรวมตามที่สอง
กฎของ Kirchhoff ถูกกำหนดโดยสูตร:
นู๋
= Nb
- นู๋
+1 – เน็ด
ที่ไหน
Nb
- จำนวนสาขาของวงจรไฟฟ้า
หนู
— จำนวนโหนด;
เน็ด
คือจำนวนของแหล่งกำเนิดแรงเคลื่อนไฟฟ้าในอุดมคติ
รูปที่ 18 ภาพประกอบ
กฎข้อที่สองของ Kirchhoff
สำหรับ,
เพื่อเขียนกฎข้อที่สองให้ถูกต้อง
Kirchhoff สำหรับรูปร่างที่กำหนดดังนี้
ปฏิบัติตามกฎต่อไปนี้:
-
โดยพลการ
เลือกทิศทางของบายพาสรูปร่าง
ตัวอย่างเช่น ตามเข็มนาฬิกา (รูปที่ 18) -
แรงเคลื่อนไฟฟ้า
และแรงดันตกที่ตรงกัน
ในทิศทางที่มีทิศทางที่เลือก
บายพาสเขียนในนิพจน์ด้วย
ลงชื่อ "+"; ถ้า e.f.s. และแรงดันตก
ไม่ตรงกับทิศทาง
รูปร่างแล้วนำหน้าด้วยเครื่องหมาย
«-».
ตัวอย่างเช่น,
สำหรับรูปร่างของรูปที่ 18 กฎข้อที่สองของ Kirchhoff
จะเขียนดังนี้
ยู1
- ยู2
+ คุณ3
= อี1
–E3
–E4
(21)
สมการ (20) สามารถเป็น
เขียนใหม่เป็น:
(อุย
– อี)
= 0 (22)
ที่ไหน
(ยู
– จ)
- ความตึงเครียดบนกิ่งไม้
เพราะเหตุนี้,
กฎข้อที่สองของ Kirchhoff สามารถกำหนดได้
ด้วยวิธีต่อไปนี้:
พีชคณิต
ผลรวมของแรงดันไฟฟ้าบนกิ่งใด ๆ
วงปิดเป็นศูนย์
ศักยภาพ
แผนภาพที่กล่าวถึงก่อนหน้านี้ ทำหน้าที่
การตีความแบบกราฟิกของวินาที
กฎของเคิร์ชฮอฟฟ์
งานหมายเลข 1
ที่
วงจรในรูปที่ 1 ได้รับกระแส I1
และฉัน3,
ความต้านทานและแรงเคลื่อนไฟฟ้า กำหนดกระแส
ฉัน4,
ฉัน5,
ฉัน6
; แรงดันไฟฟ้าระหว่างจุด a
และข
ถ้าฉัน1
= 10mA,
ฉัน3
= -20 มิลลิแอมป์,
R4
= 5kOhm,
อี5
= 20B,
R5
= 3kOhm,
อี6
= 40B,
R6
= 2kOhm.
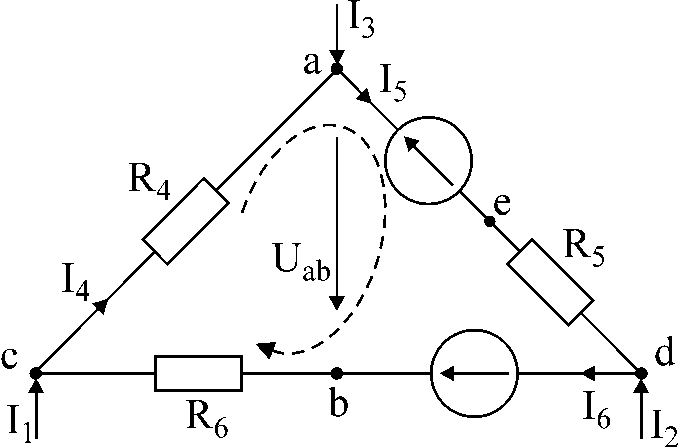
รูปที่ 1
วิธีการแก้:
-
สำหรับให้
รูปร่างเราเขียนสองสมการตาม
กฎข้อที่หนึ่งของ Kirchhoff และกฎข้อหนึ่ง - ตาม
ที่สอง. ทิศทางของรูปร่าง
ระบุด้วยลูกศร

ที่
จากผลลัพธ์ของการแก้ปัญหาที่เราได้รับ: I6
= 0; ฉัน4
= 10mA;
ฉัน5
= -10mA
-
ถาม
ทิศทางแรงดันไฟฟ้าระหว่างจุด
เอ
และข
จากจุด "ก"
เพื่อชี้ "b"
- ยูอะบี.
หาแรงดันได้จากสมการ
กฎข้อที่สองของ Kirchhoff:
ฉัน4R4
+ คุณอะบี
+ ฉัน6R6
= 0
ยูอะบี
= - 50V.
งานหมายเลข 2
สำหรับ
ไดอะแกรมในรูปที่ 2 วาดสมการตาม
กฎของ Kirchhoff และกำหนดสิ่งที่ไม่รู้
คะแนน
ที่ให้ไว้:
ฉัน1
= 20mA;
ฉัน2
= 10mA
R1
= 5kOhm,
R3
= 4kOhm,
R4
= 6kOhm,
R5
= 2kOhm,
R6
= 4kΩ
รูปที่ 2
วิธีการแก้:
จำนวนโหนด
สมการ - 3 จำนวนสมการเส้นชั้นความสูง
– 1.
จดจำ!
เมื่อรวบรวมสมการตามที่สอง
กฎของ Kirchhoff เราเลือกรูปร่างใน
ซึ่งไม่รวมถึงแหล่งที่มาปัจจุบัน
ทิศทางของรูปร่างจะแสดงในรูป
ที่
ของวงจรนี้กระแสของกิ่ง I1
และฉัน2.
ไม่รู้จัก
กระแสน้ำ
ฉัน3,
ฉัน4,
ฉัน5,
ฉัน6.

กำลังตัดสินใจ
ระบบ เราได้รับ: I3
= 13.75 มิลลิแอมป์;
ฉัน4
= -3.75mA;
ฉัน5
= 6.25mA;
ฉัน6
= 16.25mA.
แนวคิดพื้นฐาน
กระแสไฟฟ้าไหลเมื่อวงจรปิดยอมให้อิเล็กตรอนเคลื่อนที่จากศักย์สูงไปยังค่าที่ต่ำกว่าในวงจร กล่าวอีกนัยหนึ่ง กระแสต้องการแหล่งของอิเล็กตรอนที่มีพลังงานเพื่อให้พวกมันเคลื่อนที่ เช่นเดียวกับจุดที่จะกลับคืนมาของประจุลบ ซึ่งมีลักษณะเฉพาะโดยความบกพร่องของพวกมัน ตามปรากฏการณ์ทางกายภาพ กระแสในวงจรมีลักษณะเฉพาะด้วยปริมาณพื้นฐานสามประการ:
- แรงดันไฟฟ้า;
- ความแรงในปัจจุบัน
- ความต้านทานของตัวนำที่อิเล็กตรอนเคลื่อนที่
ความแข็งแกร่งและความตึงเครียด
ความแรงของกระแส (I วัดเป็นแอมแปร์) คือปริมาตรของอิเล็กตรอน (ประจุ) ที่เคลื่อนที่ผ่านตำแหน่งหนึ่งในวงจรต่อหน่วยเวลากล่าวอีกนัยหนึ่ง การวัด I คือการกำหนดจำนวนอิเล็กตรอนที่เคลื่อนที่
สิ่งสำคัญคือต้องเข้าใจว่าคำนี้หมายถึงการเคลื่อนที่เท่านั้น: ประจุไฟฟ้าสถิต เช่น บนขั้วของแบตเตอรี่ที่ไม่ได้เชื่อมต่อ ไม่มีค่าที่วัดได้ของ I กระแสที่ไหลในทิศทางเดียวเรียกว่าตรง (DC) และ การเปลี่ยนทิศทางเป็นระยะเรียกว่า alternating (AC) แรงดันสามารถอธิบายได้โดยปรากฏการณ์เช่นความดันหรือความแตกต่างในพลังงานศักย์ของวัตถุภายใต้อิทธิพลของแรงโน้มถ่วง
ในการสร้างความไม่สมดุลนี้ คุณต้องใช้พลังงานก่อน ซึ่งจะถูกรับรู้ในการเคลื่อนไหวภายใต้สถานการณ์ที่เหมาะสม ตัวอย่างเช่น เมื่อโหลดจากที่สูง งานจะดำเนินการเพื่อยกขึ้นในแบตเตอรี่กัลวานิกความต่างศักย์ที่ขั้วเกิดขึ้นเนื่องจากการแปลงพลังงานเคมีในเครื่องกำเนิดไฟฟ้า - อันเป็นผลมาจากการสัมผัสกับ สนามแม่เหล็กไฟฟ้า
ความเครียดสามารถอธิบายได้โดยปรากฏการณ์ เช่น ความดัน หรือความแตกต่างของพลังงานศักย์ของวัตถุภายใต้อิทธิพลของแรงโน้มถ่วง ในการสร้างความไม่สมดุลนี้ คุณต้องใช้พลังงานก่อน ซึ่งจะถูกรับรู้ในการเคลื่อนไหวภายใต้สถานการณ์ที่เหมาะสม ตัวอย่างเช่น เมื่อโหลดจากที่สูง งานยกจะรับรู้ ในแบตเตอรี่กัลวานิก ความต่างศักย์ที่ขั้วเกิดขึ้นเนื่องจากการแปลงของพลังงานเคมี ในเครื่องกำเนิดไฟฟ้า - อันเป็นผลมาจากการสัมผัสกับ สนามแม่เหล็กไฟฟ้า
ความต้านทานตัวนำ
ไม่ว่าตัวนำธรรมดาจะดีแค่ไหนก็ตาม อิเล็กตรอนจะไม่มีวันยอมให้อิเล็กตรอนผ่านไปได้หากไม่มีการต้านทานการเคลื่อนที่ของพวกมันเป็นไปได้ที่จะพิจารณาความต้านทานเป็นอะนาล็อกของแรงเสียดทานทางกล แม้ว่าการเปรียบเทียบนี้จะไม่สมบูรณ์แบบ เมื่อกระแสไหลผ่านตัวนำ ความต่างศักย์บางอย่างจะถูกแปลงเป็นความร้อน ดังนั้นจะมีแรงดันตกคร่อมตัวต้านทานเสมอ เครื่องทำความร้อนไฟฟ้า เครื่องเป่าผม และอุปกรณ์อื่นๆ ที่คล้ายคลึงกันได้รับการออกแบบมาเพื่อกระจายพลังงานไฟฟ้าในรูปของความร้อนเท่านั้น
ความต้านทานแบบง่าย (แสดงเป็น R) คือการวัดว่าการไหลของอิเล็กตรอนถูกหน่วงในวงจรมากเพียงใด มีหน่วยวัดเป็นโอห์ม ค่าการนำไฟฟ้าของตัวต้านทานหรือองค์ประกอบอื่นถูกกำหนดโดยคุณสมบัติสองประการ:
- เรขาคณิต;
- วัสดุ.
รูปร่างมีความสำคัญสูงสุด ดังที่เห็นได้ชัดจากการเปรียบเทียบแบบไฮดรอลิก: การผลักน้ำผ่านท่อที่ยาวและแคบนั้นยากกว่าการผลักน้ำผ่านท่อที่สั้นและกว้างมาก วัสดุมีบทบาทชี้ขาด ตัวอย่างเช่น อิเล็กตรอนสามารถเคลื่อนที่ได้อย่างอิสระในลวดทองแดง แต่ไม่สามารถไหลผ่านฉนวน เช่น ยาง ได้เลย ไม่ว่ารูปร่างของอิเล็กตรอนจะเป็นอย่างไร นอกจากรูปทรงและวัสดุแล้ว ยังมีปัจจัยอื่นๆ ที่ส่งผลต่อการนำไฟฟ้าอีกด้วย
การตีความกฎหมายของโอห์ม
คุณต้องปิดวงจรเพื่อให้แน่ใจว่ามีการเคลื่อนที่ของประจุ ในกรณีที่ไม่มีพลังงานเพิ่มเติม กระแสไฟฟ้าไม่สามารถอยู่ได้นาน ศักยภาพจะเท่าเทียมกันอย่างรวดเร็ว เพื่อรักษาโหมดการทำงานของวงจร จำเป็นต้องใช้แหล่งข้อมูลเพิ่มเติม (เครื่องกำเนิดไฟฟ้า, แบตเตอรี่)
วงจรที่สมบูรณ์จะมีความต้านทานไฟฟ้ารวมของส่วนประกอบทั้งหมด สำหรับการคำนวณที่แม่นยำ ให้คำนึงถึงการสูญเสียของตัวนำ ส่วนประกอบต้านทาน และแหล่งพลังงาน
ต้องใช้แรงดันไฟฟ้าเท่าใดสำหรับความแรงของกระแสที่กำหนดโดยสูตร:
U=I*R.
ในทำนองเดียวกันด้วยความช่วยเหลือของความสัมพันธ์ที่พิจารณาแล้วพารามิเตอร์อื่น ๆ ของวงจรจะถูกกำหนด
การเชื่อมต่อแบบขนานและแบบอนุกรม
ในทางไฟฟ้า องค์ประกอบต่างๆ จะเชื่อมต่อกันเป็นอนุกรม - ต่อจากกัน หรือขนานกัน - นี่คือเมื่ออินพุตหลายตัวเชื่อมต่อกับจุดหนึ่ง และเอาต์พุตจากองค์ประกอบเดียวกันจะเชื่อมต่อกับอีกจุดหนึ่ง
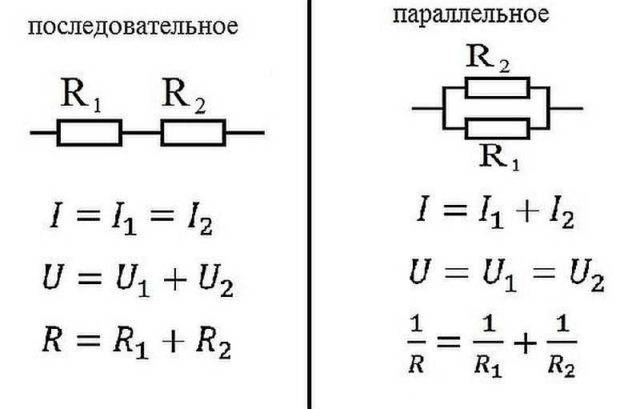
กฎของโอห์มสำหรับการเชื่อมต่อแบบขนานและแบบอนุกรม
การเชื่อมต่อแบบอนุกรม
กฎของโอห์มทำงานอย่างไรสำหรับกรณีเหล่านี้ เมื่อต่อเป็นอนุกรม กระแสที่ไหลผ่านสายโซ่ของธาตุจะเท่ากัน แรงดันไฟฟ้าของส่วนของวงจรที่มีองค์ประกอบเชื่อมต่อแบบอนุกรมคำนวณเป็นผลรวมของแรงดันไฟฟ้าในแต่ละส่วน สิ่งนี้สามารถอธิบายได้อย่างไร? การไหลของกระแสผ่านองค์ประกอบคือการถ่ายโอนส่วนหนึ่งของประจุจากส่วนหนึ่งไปยังอีกส่วนหนึ่ง ฉันหมายความว่ามันเป็นงานบางอย่าง ขนาดของงานนี้คือความตึงเครียด นี่คือความหมายทางกายภาพของความเครียด ถ้าชัดเจน เราก็ไปต่อ
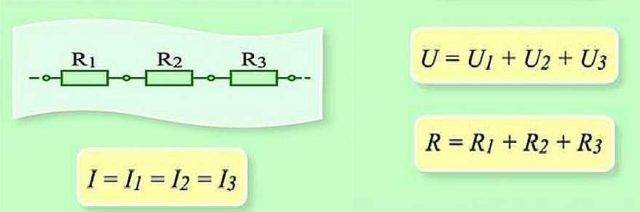
การเชื่อมต่อแบบอนุกรมและพารามิเตอร์ของส่วนนี้ของวงจร
เมื่อเชื่อมต่อเป็นอนุกรมจำเป็นต้องโอนประจุผ่านแต่ละองค์ประกอบ และในแต่ละองค์ประกอบ นี่คือ "ปริมาณ" ของงาน และในการหาปริมาณงานในส่วนทั้งหมดของห่วงโซ่ คุณต้องเพิ่มงานในแต่ละองค์ประกอบ ปรากฎว่าแรงดันไฟฟ้ารวมคือผลรวมของแรงดันไฟฟ้าในแต่ละองค์ประกอบ
ในทำนองเดียวกัน - ด้วยความช่วยเหลือเพิ่มเติม - พบความต้านทานรวมของส่วนวงจร คุณจะจินตนาการได้อย่างไร? กระแสที่ไหลผ่านสายโซ่ของธาตุจะเอาชนะแนวต้านทั้งหมดตามลำดับ ทีละคน. นั่นคือ เพื่อหาแนวต้านที่เขาเอาชนะได้ จำเป็นต้องเพิ่มแนวต้านเข้าไป มากหรือน้อยเช่นนี้อนุพันธ์ทางคณิตศาสตร์นั้นซับซ้อนกว่า และง่ายต่อการเข้าใจกลไกของกฎหมายนี้
การเชื่อมต่อแบบขนาน
การเชื่อมต่อแบบขนานคือเมื่อจุดเริ่มต้นของตัวนำ / องค์ประกอบมาบรรจบกันที่จุดหนึ่งและอีกจุดหนึ่งเชื่อมต่อกัน เราจะพยายามอธิบายกฎหมายที่ถูกต้องสำหรับสารประกอบประเภทนี้ เริ่มจากปัจจุบันกันก่อน กระแสที่มีขนาดบางกระแสถูกส่งไปยังจุดเชื่อมต่อขององค์ประกอบ มันแยกไหลผ่านตัวนำทั้งหมด จากนี้ เราสรุปได้ว่ากระแสทั้งหมดในส่วนนั้นเท่ากับผลรวมของกระแสในแต่ละองค์ประกอบ: I = I1 + I2 + I3
ตอนนี้สำหรับแรงดันไฟฟ้า หากแรงดันไฟฟ้าทำงานเพื่อเคลื่อนย้ายประจุ งานที่จำเป็นในการย้ายประจุหนึ่งครั้งจะเหมือนกันในทุกองค์ประกอบ นั่นคือแรงดันไฟฟ้าของแต่ละองค์ประกอบที่เชื่อมต่อแบบขนานจะเท่ากัน U=U1=U2=U3. ไม่สนุกและเห็นภาพเหมือนในกรณีของการอธิบายกฎของโอห์มสำหรับส่วนลูกโซ่ แต่คุณสามารถเข้าใจได้
กฎหมายสำหรับการเชื่อมต่อแบบขนาน
สำหรับการต่อต้าน สิ่งต่าง ๆ ซับซ้อนกว่าเล็กน้อย มาแนะนำแนวคิดเรื่องการนำไฟฟ้า นี่เป็นลักษณะเฉพาะที่บ่งบอกว่าประจุผ่านตัวนำนี้ง่ายหรือยากเพียงใด เป็นที่ชัดเจนว่ายิ่งความต้านทานต่ำเท่าไหร่ก็จะยิ่งผ่านได้ง่ายขึ้นเท่านั้น ดังนั้นค่าการนำไฟฟ้า - G - คำนวณเป็นส่วนกลับของความต้านทาน ในสูตรจะมีลักษณะดังนี้: G = 1/R
ทำไมเราถึงพูดถึงการนำไฟฟ้า? เนื่องจากค่าการนำไฟฟ้าทั้งหมดของส่วนที่มีการเชื่อมต่อแบบขนานขององค์ประกอบเท่ากับผลรวมของค่าการนำไฟฟ้าสำหรับแต่ละส่วน G = G1 + G2 + G3 - เข้าใจง่าย กระแสจะเอาชนะโหนดขององค์ประกอบคู่ขนานนี้ได้ง่ายเพียงใดขึ้นอยู่กับการนำไฟฟ้าของแต่ละองค์ประกอบ เลยกลายเป็นว่าต้องพับเก็บ
ตอนนี้เราสามารถเข้าสู่แนวต้านได้แล้วเนื่องจากค่าการนำไฟฟ้าเป็นส่วนกลับของความต้านทาน เราจึงได้สูตรต่อไปนี้: 1/R = 1/R1 + 1/R2 + 1/R3
อะไรทำให้เรามีการเชื่อมต่อแบบขนานและแบบอนุกรม
ความรู้เชิงทฤษฎีนั้นดี แต่จะนำไปใช้ในทางปฏิบัติอย่างไร? องค์ประกอบประเภทใดก็ได้สามารถเชื่อมต่อแบบขนานและแบบอนุกรมได้ แต่เราพิจารณาเฉพาะสูตรที่ง่ายที่สุดที่อธิบายองค์ประกอบเชิงเส้น องค์ประกอบเชิงเส้นคือความต้านทานซึ่งเรียกอีกอย่างว่า "ตัวต้านทาน" นี่คือวิธีที่คุณสามารถใช้สิ่งที่คุณได้เรียนรู้:
หากไม่มีตัวต้านทานค่าสูง แต่มีตัวต้านทานน้อยกว่าหลายตัว สามารถรับค่าความต้านทานที่ต้องการได้โดยเชื่อมต่อตัวต้านทานหลายตัวเป็นอนุกรม อย่างที่คุณเห็น นี่เป็นเทคนิคที่มีประโยชน์
เพื่อยืดอายุการใช้งานของแบตเตอรี่ สามารถเชื่อมต่อแบบขนานได้ แรงดันไฟฟ้าในกรณีนี้ตามกฎของโอห์มจะยังคงเท่าเดิม (คุณสามารถตรวจสอบได้โดยการวัดแรงดันไฟฟ้าด้วยมัลติมิเตอร์) และ "อายุการใช้งาน" ของแบตเตอรี่คู่จะยาวนานกว่าสององค์ประกอบที่จะมาแทนที่กัน
โปรดทราบ: เฉพาะอุปกรณ์จ่ายไฟที่มีศักยภาพเท่ากันเท่านั้นที่สามารถเชื่อมต่อแบบขนานได้ นั่นคือไม่สามารถเชื่อมต่อแบตเตอรี่ที่ตายแล้วและใหม่ได้
หากคุณยังคงเชื่อมต่ออยู่ แบตเตอรี่ที่มีประจุมากขึ้นมักจะชาร์จแบตเตอรี่ที่มีประจุน้อยกว่า เป็นผลให้ค่าใช้จ่ายทั้งหมดของพวกเขาลดลงเป็นมูลค่าต่ำ
โดยทั่วไป สิ่งเหล่านี้เป็นการใช้ทั่วไปสำหรับสารประกอบเหล่านี้
แหล่ง EMF ในอุดมคติ
แรงเคลื่อนไฟฟ้า (E) คือปริมาณทางกายภาพที่กำหนดระดับอิทธิพลของแรงภายนอกต่อการเคลื่อนที่ในวงจรปิดของตัวพาประจุ กล่าวอีกนัยหนึ่งว่ากระแสที่ไหลผ่านตัวนำนั้นแรงแค่ไหนจะขึ้นอยู่กับ EMF
เมื่ออธิบายปรากฏการณ์ที่เข้าใจยากเช่นนี้ ครูโรงเรียนในประเทศชอบใช้วิธีเปรียบเทียบแบบไฮดรอลิกส์ หากตัวนำเป็นท่อ และกระแสไฟฟ้าคือปริมาณน้ำที่ไหลผ่าน EMF คือแรงดันที่ปั๊มพัฒนาเพื่อสูบของเหลว
คำว่าแรงเคลื่อนไฟฟ้าเกี่ยวข้องกับแนวคิดเช่นแรงดันไฟฟ้า เธอยังวัด EMF เป็นโวลต์ (หน่วย - "V") แหล่งพลังงานทุกแหล่ง ไม่ว่าจะเป็นแบตเตอรี่ เครื่องกำเนิดไฟฟ้า หรือแผงโซลาร์เซลล์ มีแรงเคลื่อนไฟฟ้าในตัวเอง บ่อยครั้งที่ EMF นี้อยู่ใกล้กับแรงดันเอาต์พุต (U) แต่น้อยกว่านั้นเล็กน้อยเสมอ สาเหตุนี้เกิดจากความต้านทานภายในของแหล่งกำเนิด ซึ่งส่วนหนึ่งของแรงดันไฟฟ้าจะลดลงอย่างหลีกเลี่ยงไม่ได้
ด้วยเหตุผลนี้ แหล่งกำเนิด EMF ในอุดมคติจึงเป็นแนวคิดที่เป็นนามธรรมหรือแบบจำลองทางกายภาพที่ไม่มีอยู่ในโลกแห่งความเป็นจริง เนื่องจากความต้านทานภายในของแบตเตอรี่ Rin แม้ว่าจะต่ำมาก แต่ก็ยังแตกต่างจากศูนย์สัมบูรณ์
แหล่งที่มาของแรงเคลื่อนไฟฟ้าในอุดมคติและแท้จริง
ในรูปแบบดิฟเฟอเรนเชียล
สูตรนี้มักถูกนำเสนอในรูปแบบดิฟเฟอเรนเชียล เนื่องจากตัวนำมักจะไม่เป็นเนื้อเดียวกัน และจำเป็นต้องแบ่งมันออกเป็นส่วนที่เล็กที่สุดเท่าที่จะเป็นไปได้ กระแสที่ไหลผ่านนั้นสัมพันธ์กับขนาดและทิศทาง ดังนั้นจึงถือว่าเป็นปริมาณสเกลาร์ เมื่อใดก็ตามที่พบกระแสที่เป็นผลลัพธ์ผ่านเส้นลวด ผลรวมเชิงพีชคณิตของกระแสทั้งหมดจะถูกนำมา เนื่องจากกฎนี้ใช้เฉพาะกับปริมาณสเกลาร์ กระแสจึงถือเป็นปริมาณสเกลาร์ด้วย เป็นที่ทราบกันว่า dI = jdS ปัจจุบันผ่านส่วน แรงดันไฟฟ้าของมันคือ Edl จากนั้นสำหรับลวดที่มีหน้าตัดคงที่และมีความยาวเท่ากัน อัตราส่วนจะเป็นจริง:
 รูปแบบดิฟเฟอเรนเชียล
รูปแบบดิฟเฟอเรนเชียล
ดังนั้นนิพจน์ของกระแสในรูปแบบเวกเตอร์จะเป็น: j = E.
สำคัญ! ในกรณีของตัวนำโลหะ ค่าการนำไฟฟ้าจะลดลงตามอุณหภูมิที่เพิ่มขึ้น ในขณะที่สารกึ่งตัวนำจะเพิ่มขึ้น กฎของ Omov ไม่ได้แสดงให้เห็นถึงสัดส่วนที่เข้มงวด
ความต้านทานของโลหะและโลหะผสมกลุ่มใหญ่จะหายไปที่อุณหภูมิใกล้กับศูนย์สัมบูรณ์ และกระบวนการนี้เรียกว่าตัวนำยิ่งยวด